Was kann man am Einheitskreis ablesen?
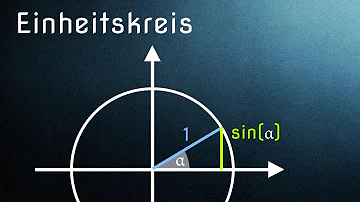
Trägt man an der x-Achse einen Winkel α an, kann man mithilfe des Einheitskreises die Werte des Sinus und Kosinus von α ablesen.
Was sagt der Einheitskreis aus?
Im Einheitskreis entspricht die Gegenkathete dem Sinuswert und die Ankathete dem Kosinuswert, wobei auf die Vorzeichen zu achten ist. Ebenfalls gilt: Die Koordinaten des Punktes P auf der Kreislinie des Einheitskreises geben Kosinuswert (x) und Sinuswert (y) an.
Was kann man mit dem Einheitskreis machen?
Mit Hilfe des Einheitskreises kannst du die Definition der Winkelfunktionen Sinus, Cosinus und Tangens auf alle Winkel erweitern. Zusätzlich erlaubt er dir die charakteristischen Kurven dieser Winkelfunktionen zu konstruieren. Einheitskreis in einem Koordinatensystem.
Wie kann man den Tangens am Einheitskreis ablesen?
Vom Einheitskreis zur Winkelfunktion
Die Bezeichnung "Tangens" ergibt sich aus dem Begriff Tangente. Der Tangens entspricht der Länge der pinken Strecke, die auf der Tangente des Einheitskreises im Punkt 1 | 0 liegt. Beachte aber: Es ist üblich, für das Argument einer Funktion die Variable x zu verwenden.
Wann liegt ein Punkt auf dem Einheitskreis?
Zu jedem Winkel α zwischen 0° und 360° gehört ein Punkt P auf dem Einheitskreis mit den Koordinaten (x|y).
Ist der Einheitskreis eine Funktion?
Winkelfunktionen für alle Winkel definiert
Mithilfe des Einheitskreises können wir jedoch zeigen, dass die Winkelfunktionen für jeden beliebigen (positiven und negativen) Winkel definiert sind.
Wann sind sin und COS gleich?
Wähle einen beliebigen Winkel α und überprüfe die Gleichheit mit deinem Taschenrechner. Mit Hilfe dieser Beziehung kannst du ohne Taschenrechner zu jedem Winkel den Sinus aus dem Kosinus oder den Kosinus aus dem Sinus bestimmen. Wenn sin(α)=0.6 , dann cos(α)=0.8 .
Welchen Radius hat der Einheitskreis?
Hinführung. Ein Kreis, dessen Radius die Länge r = 1 LE hat, ist ein Einheitskreis. In einem kartesischen Koordinatensystem liegt sein Mittelpunkt im Ursprung. Ein Winkel im Einheitskreis hat seinen Scheitelpunkt im Ursprung.
Warum kein tan 90?
Tangens nicht definiert
Ihre Werte gehen von -1 bis +1 . Der Tangens kann hingegen auch nicht definiert sein. Dies ist der Fall, wenn x=0 ist, unsere Ankathete also keine Länge hat. Dies ist bei 90° der Fall, bei 270° , bei 450° usw.
Was ist Pi im Einheitskreis?
Der Punkt M wird Mittelpunkt des Kreises mit dem Radius r genannt. Um den Umfang, also die Länge der Kreislinie zu berechnen benötigt man die sogenannte Kreiszahl Pi: π = 3,14159… Mithilfe der obigen Formel lässt sich die Länge der gesamten Kreislinie berechnen.
Was ist der Sinus im Einheitskreis?
Definition von Sinus, Kosinus am Einheitskreis. Zu jedem Winkel α in einem Kreis mit dem Radius 1 (Einheitskreis), dessen Scheitelpunkt der Nullpunkt ist und der den positiven Strahl der x-Achse als einen Schenkel hat, gehört ein zweiter Schenkel, der den Kreis in einem Punkt P schneidet.
Warum ist der Sinus von 90 Grad 1?
Bei einem Winkel von 90° ist die Gegenkathete genauso lang wie die Hypotenuse. Das heißt, wir berechnen sin(90°) = (GK)/HY = (HY)/HY = 1 . Daher ist sin(90°) = 1 .
Was sagt der Sinus aus?
Der Sinus eines Winkels ist das Verhältnis der Länge der Gegenkathete (Kathete, die dem Winkel gegenüberliegt) zur Länge der Hypotenuse (Seite gegenüber dem rechten Winkel). Der Kosinus ist das Verhältnis der Länge der Ankathete (das ist jene Kathete, die einen Schenkel des Winkels bildet) zur Länge der Hypotenuse.
Was ist der Sinus von 1?
Bei einem Winkel von 90° ist die Gegenkathete genauso lang wie die Hypotenuse. Das heißt, wir berechnen sin(90°) = (GK)/HY = (HY)/HY = 1 . Daher ist sin(90°) = 1 .
Wo ist COS 0?
Bei einem Winkel von 0° ist die Ankathete genauso lang wie die Hypotenuse. Das heißt, wir berechnen cos(0°) = (AK)/HY = (HY)/HY = 1 . Daher ist cos(90°) = 1 . Bei einem Winkel von 90° hat die Ankathete eine Länge von 0 .
Was drückt Pi aus?
Die Kreiszahl Pi hat das Symbol pi. Sie ist eine mathematische Konstante, die das Verhältnis zwischen dem Umfang eines Kreises zu seinem Durchmesser beschreibt. Wir benötigen diese Zahl in allen möglichen Formeln rund um kreisförmige Berechnungen, aber auch in anderen Bereichen der Mathematik und Physik.
Warum sind 360 Grad 2 Pi?
Umrechnung zwischen Grad und Radiant
Eine volle Umdrehung in Radiant ausgedrückt entspricht der Länge des Umfanges des Einheitskreises. Diese Länge beträgt genau 2π. Eine volle Umdrehung im Kreis entspricht also 360 Grad oder 2π Radiant (rad). Gleichsetzen dieser beiden Terme ergibt 2π rad=360∘.
Was drückt der Sinus aus?
- Der Sinus ist eine sogenannte Winkelfunktion. Der Sinus ist an und für sich unanschaulich. Er drückt aber im rechtwinkligen Dreieck das Verhältnis zwischen Gegenkathete und Hypotenuse aus, so dass man damit eine Beziehung zwischen Winkeln und den Seitenlängen des Dreiecks erhält.
Wann sind COS und sin gleich?
Beziehung trigonometrischer Funktionen
| Sinus | Cosinus | Tangens |
|---|---|---|
| sin(180°+α)=-sin(α) | cos(180°+α)=-cos(α) | tan(180°+α)=tan(α) |
| sin(180°-α)=sin(α) | cos(180°-α)=-cos(α) | tan(180°-α)=-tan(α) |
| sin(360°-α)=-sin(α) | cos(360°-α)=cos(α) | tan(360°-α)=-tan(α) |
Jul 28, 2021
Wie berechnet man sin ohne Taschenrechner?
- sin²(α) + cos²(α) = 1
Mit Hilfe dieser Beziehung kannst du ohne Taschenrechner zu jedem Winkel den Sinus aus dem Kosinus oder den Kosinus aus dem Sinus bestimmen. Wenn sin(α)=0.6 , dann cos(α)=0.8 .
Wann ist der sin 0?
Bei einem Winkel von 0° hat die Gegenkathete eine Länge von 0 . Wir berechnen sin(0°) = GK/HY = 0/HY = 0 . Daher ist sin(0°) = 0 .
Wie lese ich eine Sinusfunktion ab?
Die Sinusfunktion ist eine trigonometrische Funktion. Sie ordnet einem x-Wert seinen Sinuswert als y zu: y = sin(x). Du kannst die Sinuswerte auch am Einheitskreis ablesen.
Für was braucht man Sinus?
Mit dem Sinus kann man entweder die Länge der Hypotenuse oder die Länge der Gegenkathete oder die Größe des Winkels berechnen, je nachdem, welche der drei Größen gesucht ist. Die jeweils anderen beiden Größen müssen gegeben sein.
Wo ist sin 0?
Bei einem Winkel von 0° hat die Gegenkathete eine Länge von 0 . Wir berechnen sin(0°) = GK/HY = 0/HY = 0 . Daher ist sin(0°) = 0 .
Für was braucht man sin?
Der Sinus, der Cosinus und der Tangens werden angewendet, um Winkel und Seiten rechtwinkliger Dreiecke zu bestimmen.
Warum ist Sinus 90 Grad 1?
Bei einem Winkel von 90° ist die Gegenkathete genauso lang wie die Hypotenuse. Das heißt, wir berechnen sin(90°) = (GK)/HY = (HY)/HY = 1 . Daher ist sin(90°) = 1 .
